什么是线性查找法

你面前有一堆试卷，你要通过自己的学号，在其中找到自己的试卷，你会从第一张开始，一张张比对。直到找到学号一致的试卷为止

实现线性查找法

查询目标是否在对应的数组中，存在则返回对应的下标，不是则返回-1

代码

public class LinearSearch {

    private LinearSearch() {
    }
    // 避免重复创建，直接使用泛型
    public static  int search(T[] data, T target) {
        for (int i = 0; i < data.length; i++) {
            if (target.equals(data[i])) {
                return i;
            }
        }
        return -1;
    }
}

测试

   public static void main(String[] args) {
        int n = 1000000;
        Integer[] data = ArrayGenerator.generatorOrderArray(n);
        System.out.println(LinearSearch.search(data,5));
        System.out.println(LinearSearch.search(data,101));
    }

结果

5
-1

使用自定义类测试算法

创建自定义类 Student

public class Student{

    String name;

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public Student(String name) {
        this.id = id;
        this.name = name;
    }

    @Override
    /**
    * 默认比较的是类对象的地址，所以需要重写成我们认为相同的条件
    */
    public boolean equals(Object obj) {
        if (this == obj) {
            return true;
        }
        if (obj == null) {
            return false;
        }
        if (!(obj instanceof Student)) {
            return false;
        }
        Student student = (Student) obj;
        // 我们认为名字相同，学生即为同一人
        return Objects.equals(this.name, student.getName());
    }
}

测试

public static void main(String[] args) {
        Student[] students = {new Student("a"),
                new Student("b"),
                new Student("c"),
        };
        Student student = new Student("b");
        int search = LinearSearch.search(students, student);
        System.out.println(search);
}

结果

1

循环不变量

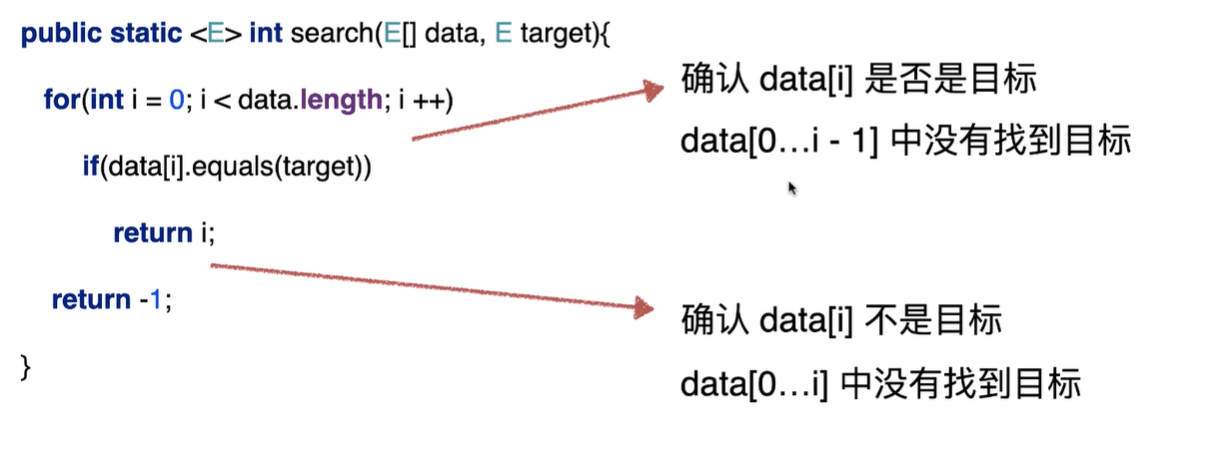
测试算法性能

使用1000000条数据进行测试

   public static void main(String[] args) {
        int n = 1000000;
        Integer[] data = ArrayGenerator.generatorOrderArray(n);
        long startTime = System.nanoTime();
        for (int k = 0; k < 100; k++) {
            LinearSearch.search(data, n);
        }
        long endTime = System.nanoTime();
        System.out.println((endTime - startTime) / 1000000000.0);
    }

结果

0.1616517

使用1000000条数据进行测试

public static void main(String[] args) {
        int n = 10000000;
        Integer[] data = ArrayGenerator.generatorOrderArray(n);
        long startTime = System.nanoTime();
        for (int k = 0; k < 100; k++) {
            LinearSearch.search(data, n);
        }
        long endTime = System.nanoTime();
        System.out.println((endTime - startTime) / 1000000000.0);
    }

结果

1.3592809

在数据量扩大了10倍的情况下，总体耗时也扩大了10倍，时间性能与数据体量成线性增长，因此可以得出此算法的时间复杂度为O(n)级别，